The DFPMIN procedure minimizes a user-written function Func of two or more independent variables using the Broyden-Fletcher-Goldfarb-Shanno variant of the Davidon-Fletcher-Powell method, using its gradient as calculated by a user-written function Dfunc.
DFPMIN is based on the routine dfpmin described in section 10.7 of Numerical Recipes in C: The Art of Scientific Computing (Second Edition), published by Cambridge University Press, and is used by permission.
DFPMIN, X, Gtol, Fmin, Func, Dfunc [, /DOUBLE] [, EPS=value] [, ITER=variable] [, ITMAX=value] [, STEPMAX=value] [, TOLX=value]
On input, X is an n-element vector specifying the starting point. On output, it is replaced with the location of the minimum.
Note: If DFPMIN is complex then only the real part is used for the computation.
An input value specifying the convergence requirement on zeroing the gradient.
On output, Fmin contains the value at the minimum-point X of the user-supplied function specified by Func.
A scalar string specifying the name of a user-supplied IDL function of two or more independent variables to be minimized. This function must accept a vector argument X and return a scalar result.
For example, suppose we wish to find the minimum value of the function
y = (x0 – 3)4 + (x1 – 2)2
To evaluate this expression, we define an IDL function named MINIMUM:
FUNCTION minimum, X
RETURN, (X[0] - 3.0)^4 + (X[1] - 2.0)^2
END
A scalar string specifying the name of a user-supplied IDL function that calculates the gradient of the function specified by Func. This function must accept a vector argument X and return a vector result.
For example, the gradient of the above function is defined by the partial derivatives:
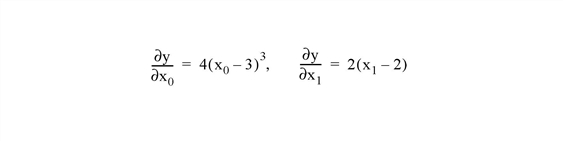
We can write a function GRAD to express these relationships in the IDL language:
FUNCTION grad, X
RETURN, [4.0*(X[0] - 3.0)^3, 2.0*(X[1] - 2.0)]
END
Set this keyword to force the computation to be done in double-precision arithmetic.
Use this keyword to specify a number close to the machine precision. For single-precision calculations, the default value is 3.0 x 10-8. For double-precision calculations, the default value is 3.0 x 10-16.
Use this keyword to specify a named variable which returns the number of iterations performed.
Use this keyword to specify the maximum number of iterations allowed. The default value is 200.
Use this keyword to specify the scaled maximum step length allowed in line searches. The default value is 100.0
Use this keyword to specify the convergence criterion on X values. The default value is 4 x EPS.
To minimize the function MINIMUM:
PRO example_dfpmin
; Make an initial guess (the algorithm’s starting point):
X = [1.0, 1.0]
; Set the convergence requirement on the gradient:
Gtol = 1.0e-7
; Find the minimizing value:
DFPMIN, X, Gtol, Fmin, 'minimum', 'grad'
; Print the minimizing value:
PRINT, X
END
FUNCTION minimum, X
RETURN, (X[0] - 3.0)^4 + (X[1] - 2.0)^2
END
FUNCTION grad, X
RETURN, [4.0*(X[0] - 3.0)^3, 2.0*(X[1] - 2.0)]
END
IDL prints:
3.00175 2.00000
|
4.0 |
Introduced |